恰同学少年

过拟合：当学习器把训练样本学得“太好”了的时候，很可能已经把样本自身的一些特点当作了所有潜在样本都会具有的一般性质，这样就会导致泛化性能下降，这种现象被称为过拟合（over-fitting）；过拟合是机器学习面临的关键障碍，各类学习算法都必然带有一些针对过拟合的措施，然而必须认识到，过拟合是无法彻底避免的，我们能做到的只是“缓解”，或者说减少其风险；可以这样理解：机器学习面临的问题通常是NP难甚至更难，而有效的学习算法必然是在多项式时间内运行完成，若可彻底避免过拟合，则通过经验误差最小化就能获得最优解，这就意味着我们构造性地证明了“P=NP”；因此，只要相信“P!=NP”，过拟合就不可避免； 避免过拟合（高方差）

获取更多的训练样本；
尝试使用更少的特征的集合；
尝试增加 λ（正则惩罚项）；

欠拟合：指对训练样本的一般性质尚未学好；欠拟合比较容易克服，比如在决策树学习中扩展分支，在神经网络学习中增加训练轮数等； 避免欠拟合（高偏差）

尝试获得其他特征；
尝试添加多项组合特征；
尝试减小 λ （正则惩罚项）；

3. 评估方法

一般使用一个“测试集”来测试学习器对新样本的判别能力，然后以测试集上的测试误差作为泛化误差的近似。训练集和测试集的划分如下：

3.1 留出法（hold-out）

在保持数据分布的一致性的基础上，将数据集划分成两个互斥的集合，一个训练一个测试；通常的做法是将大约2/3~4/5的样本用于训练，剩余样本用于测试（一般而言，测试集至少应含30个样例）。而且一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果；缺陷：数据集如何划分会影响评估结果的稳定性和保真性；

3.2 交叉验证法（cross validation，k折交叉验证）

在保持数据分布一致性的基础上，将数据集划分为k个大小相似的互斥子集，每次用k-1个子集的并集作为训练集，剩下的一个子集作为测试集，进行k次训练和测试，最终返回的是这k个测试结果的均值（k最常用的取值是10，其他常用的有5，20等）；由于数据集有多种划分方式，为了减小因样本划分不同而引入的差别，k折交叉验证通常要随机使用不同的划分重复10次，最终的评估结果使这p次交叉验证结果的均值，例如常见的有10次10折交叉验证；

3.2.1 留一法（Leave-One-Out，简称LOO，k折交叉验证的特例）

如果数据集包含m个样本，若令k=m，则为留一法；在绝大多数情况下，留一法中被实际评估的模型与期望评估的用D训练出的模型很相似。因此，留一法的评估结果往往被认为比较准确；缺陷：数据集比较大的时候，计算开销无法忍受（比如100万）；

3.3 自助法（bootstrapping）

每次随机从数据集D（m个样本）中选择一个样本，将其拷贝到D’中，该样本仍然放入D中，重复m次，得到包含m个样本的数据集D’。D’中会有一些重复的样本，而且计算可得，初始数据集D中约有36.8%的样本未能出现在采样数据集D’中，将D’用作训练集，D\D’（\表示集合减法）用作测试集；这样保证模型由m个样本训练而成；优点：可以减少训练样本规模不同造成的影响；在数据集较小、难以有效划分训练集和测试集时很有用；缺陷：自助法产生的数据集改变了初识数据集的分布，这会引入估计偏差，因此，在初始数据量足够时，留出法和交叉验证法更常用一些；在模型评估与选择的过程中只使用了一部分数据训练模型，在模型选择完成后，学习算法和参数配置已选定，此时应该用所有数据集重新训练模型，这才是最终的模型；

3.4 训练集、测试集&&验证集

Training set: A set of examples used for learning, which is to fit the parameters [i.e., weights] of the classifier.
Validation set: A set of examples used to tune the parameters [i.e., architecture, not weights] of a classifier, for example to choose the number of hidden units in a neural network.
Test set: A set of examples used only to assess the performance [generalization] of a fully specified classifier.

简单理解如下：

训练集：训练模型；
测试集：评估模型在实际使用时的泛化性能；
验证集：模型选择和调参；

4. 性能度量

一般使用查准率、查全率与F1三个度量指标；准确率（查准率，precise）：预测为正的结果中原本就是正样本的比例；召回率（查全率，recall）：原本为正的样本中被正确预测出来的比例；查准率和查全率是一对矛盾的度量，一般来说，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低；通常只有在一些简单的任务中，才可能使查全率和查准率都很高；

5. 规范化

5.1 为什么要进行规范化？

在多指标评价体系中，由于各评价指标的性质不同，通常具有不同的量纲和数量级。当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。因此，为了保证结果的可靠性，需要对原始指标数据进行标准化处理。在标准化处理后，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

5.2 Min-max 规范化

也叫离差标准化，是对原始数据的线性变换，使结果落到[0,1]区间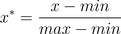；其中，max为样本数据的最大值，min为样本数据的最小值。缺陷：min-max标准化方法保留了原始数据之间的相互关系，但是如果标准化后，新输入的数据超过了原始数据的取值范围，即不在原始区间[minA, maxA]中，则会产生越界错误。因此这种方法的一个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。 适用情况：原始数据的取值范围已经确定的情况。

5.3 z-score 规范化

也叫标准差标准化，经过处理的数据符合标准正态分布，即均值为0，标准差为1，其转化函数为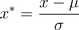：其中，μ为所有样本数据的均值，σ为所有样本数据的标准差。 适用情况：z-score规范化方法适用于属性A的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况。

5.4 log函数转换

通过以10为底的log函数转换的方法同样可以实现归一化，具体方法如下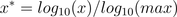：其中，max为样本数据最大值； 适用情况：所有的数据都要大于等于1。

5.5 atan函数转换

用反正切函数也可以实现数据的归一化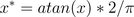：注：使用这个方法需要注意的是如果想映射的区间为[0,1]，则数据都应该大于等于0，小于0的数据将被映射到[-1,0]区间上。

6. 参考文献

啊哈！原来如此——说说数学中的趣事

发表于 2016-02-28 更新于 2019-12-22 分类于读书 Valine：

这是一本相当不错的关于数学科普的书籍，“本书从逻辑、数、几何、概率、统计以及时间等6个方面探讨了悖论的产生过程和解读角度”，书中介绍了很多常见而有趣的悖论，如“说谎者悖论”、“理发师悖论”、“芝诺悖论”等等；记得曾经在上西方哲学史的课上，老师在介绍古希腊哲学家们探讨万物本源的时候说，毕达哥拉斯认为“数是万物的本源”，当时就觉得第一次有这个认识的人真不愧是天人，从我的角度看，这是一次认知上质的飞跃，人们开始思考独立于物体表象的一般规律，这也标志着人们开始从感性的思维进入理性的思维。从本书中，更加可以验证以上观点，书中很多数学的谜题从感性的思维上来看是没有任何悖论的，然而通过数学的精准计算，就会洞悉其内在的实质。

阅读全文 »